Calculations

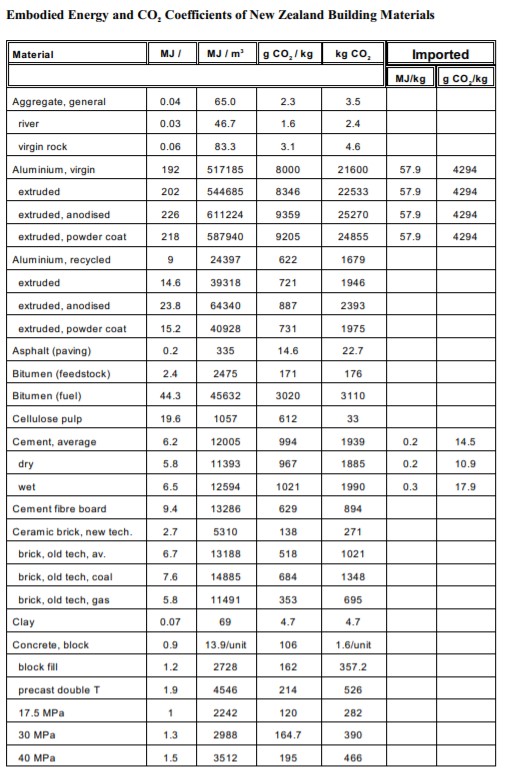
Data

For the calculation of the embodied energy each slab is divided into the different materials and the volume of each material is calculated based on the entire height. With the approximate embodied energy of each material the total embodied energy is calculated. The embodied energy for each slab is given in MJ per square meter and total height of the slab. An overview of the different materials is given in the following table.

Material	Density	MJ/m3	Assumption	Source embodied energy
Reinforced concrete	25 kN/m3
Standard concrete	24kN/m3	2600		1 and 2
High strength concrete	24kN/m3	3300		2 and 3
Reinforcement	78.5kN/m3	170000	Average of typical steel (about 42% recycled)	1 and 2
Structural steel	78.5kN/m3	170000	Average of typical steel (about 42% recycled)	1 and 2
Timber	3.8kN/m3	1300	Air dried	1 and 2

The density values are taken form the Swiss Code SIA 261. Detail to the sources from the emodied energy can be found here.

Calculation for each Slab

Content
Flat Slab
Ribbed Slab
Waffle Slab
Hollow Core
Composite Solid Prestressed Soffit Slab
Composite Lattice Prestressed Soffit Slab
Precast Double-Tees
Steel-Concrete Composite Slab
Timber-Concrete Composite Slab
Holedeck
Slim-Floor
Voided Biaxial Slab
Laminated Timber Slab

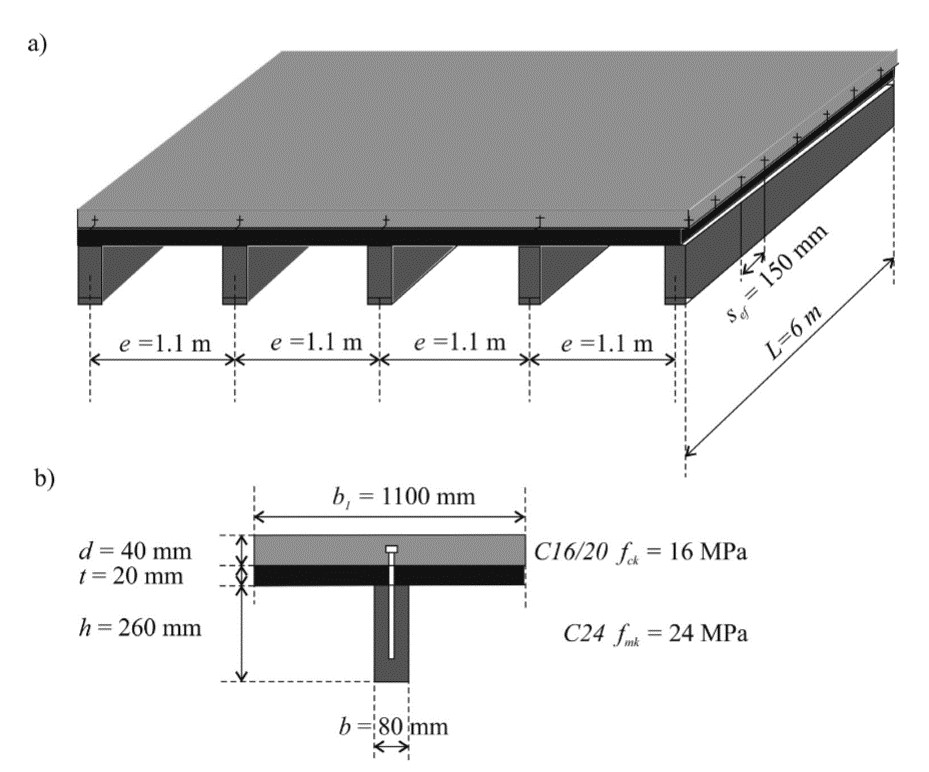
Flat Slab

Weight: 25 kN/m3 (kN per square meter and total height of slab)
The density of reinforced concrete is taken from the Swiss Code SIA 261.

Embodied energy: 5948 MJ/m3.

Volume of materials:
Standard Concrete: 98 %vol
High strength concrete: 0 %vol
Reinforcement: 2 %vol
Steel: 0 % vol
Timber: 0 %vol
Air:0 %vol

Assumptions:
For the amount of reinforcement an example with a slab thickness of 20cm and the size 1m2 is calulated. The reinforcement in the top two layers is assumed to be D10/150 (A=523mm2) and in the bottom layers D14/100 (A=1’540mm2). Therefore, the volume of concrete is 0.2m3 and the reinforcment 0.004126m3 ((2*1540 + 2*523)/1000^2). Therefore, about 2% of the volume is reinforcement.

Ribbed Slab

Weight: 8.5 kN/m3 (kN per m2 and total height of slab)
To calclate the weight two typical examples are chosen. For those examples the area of reinforced concrete is calculated and divided by the total area.

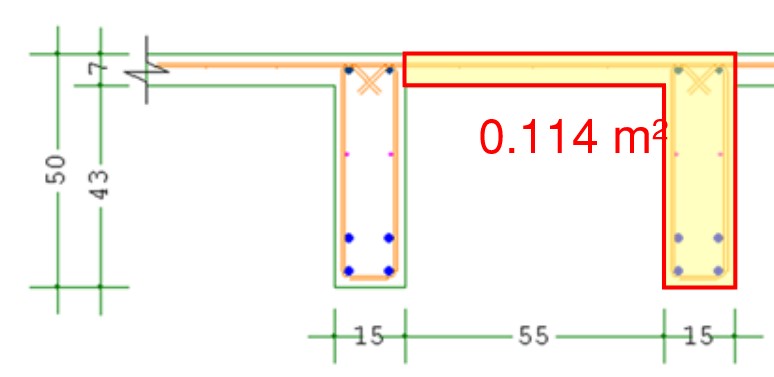
Example 1:
Area concrete: Ac = 0.114m2
Total area: A = 0.7m * 0.5m = 0.35m2
-> 0.114/0.35 * 25 kN/m3 = 8.1 kN/m3

Reference: http://www.koumoulos.com/managed_images/flyer/4b.png

Example 2:
Area concrete: Ac= 0.75*0.07 + 0.15*0.28 = 0.0945m2
Total area: A = 0.75m * 0.35m = 0.2625m2
-> 0.0945/0.2625 * 25 kN/m3 = 9.0 kN/m3

Reference: https://www.youtube.com/watch?app=desktop&v=WD6wYBniEeM

Embodied energy: 2056 MJ/m3.

Volume of materials:
Standard Concrete: 33.3 %vol
High strength concrete: 0 %vol
Reinforcement: 0.7 %vol
Steel: 0 % vol
Timber: 0 %vol
Air: 66 %vol

Assumptions:
8.5kN/m3 / 25.0 kN/m3 = 0.34
34% of the total volume is reinforced concrete and the rest air. 2% out of those 34% is reinforcement (0.7%) and the rest standard concrete.

Waffle Slab

Weight: 11.2 kN/m3 (kN per m2 and total height of slab)
For the weight calculation of the waffle slab it is assumed that the ribbes have the same spacing in both direction. Then, the weight for the squared influence area which goes from the middle of the rib to the middle of the next rib is calculated.
Influence area: Ainfl = 0.75*0.75=0.5625m2
Reinforced concrete volume: Vconc= 0.6*0.6*0.07 + (0.15/2)*0.28*(0.75*4) = 0.0882m3
Therefore the weight is: Vonc*25kN/m3 / (Ainfl*h) = 0.0882m3*25kN/m3 / (0.5625m2*0.35m) = 11.2 kN/m3

Reference: https://www.youtube.com/watch?app=desktop&v=WD6wYBniEeM

Embodied energy: 2677 MJ/m3.

Volume of materials:
Standard Concrete: 44.1 %vol
High strength concrete: 0 %vol
Reinforcement: 0.9 %vol
Steel: 0 % vol
Timber: 0 %vol
Air: 55 %vol

Assumptions:
11.2kN/m3 / 25.0 kN/m3 = 0.45
45% of volume is reinforced concrete and the rest air. 2% out of those 45% is reinforcement (0.9%) and the rest standard concrete.

Hollow Core

Weight: 14.5 kN/m3 (kN per m2 and total height of slab)
An averaged value of the following examples is used.
16.5kN/m3 (h=0.15m), 15.5kN/m3 (h=0.20m),13.7kN/m3 (h=0.26m). (https://www.bison.co.uk/products/hollowcore-floors/)
16kN/m3 (h=0.15m), 14.5kN/m3 (h=0.20m), 13.2kN/m3 (h=0.30m), 12.5kN/m3 (h=0.40m). (https://www.mannokbuild.com/precast/hollowcore-flooring/)

Embodied energy: 3164 MJ/m3.

Volume of materials:
Standard Concrete: 0 %vol
High strength concrete: 57.25 %vol
Reinforcement: 0.75%vol
Steel: 0 % vol
Timber: 0 %vol
Air: 42 %vol

Assumptions:
14.5kN/m3 / 25.0 kN/m3 = 0.58
58% of volume is prestressed high strength concrete and prestressing strands. 0.75% of the total volume is assumed to be prestressing strands. This based on an average of the following references:
Half the amount strands needed as reinforcement in a flat slab (2%). => 1% (http://www.sustainableprecast.ca/en/precast_sustainability/material_selection/
7 strands with d=15mm, total area hollow core 1.2m*0.22m=0.264m2 => 0.001237/0.264 = 0.47% (https://www.researchgate.net/publication/320660266_Numerical_Investigation_on_Detection_of_Prestress_Losses_in_a_Prestressed_Concrete_Slab_by_Modal_Analysis/figures?lo=1)
14 strands with d=15mm, total area hollow core 1.2m*0.27m=0.324m2 => 0.002474/0.264 = 0.76% (https://www.bft-international.com/en/artikel/artikel_en_864867.html)

Composite Solid Prestressed Soffit Slab

Weight: 24.0 kN/m3 (kN per m2 and total height of slab)
The producer specifies a density of 24kN/m3. (https://www.precastfloors.info/Precast/media/BPMediaLibrary/Publications/Solid-Prestressed-Composite-Floors_1.pdf?ext=.pdf)

Embodied energy: 6634 MJ/m3.

Volume of materials:
Standard Concrete: 0 %vol
High strength concrete: 98 %vol
Reinforcement: 2 %vol
Steel: 0 % vol
Timber: 0 %vol
Air: 0 %vol

Assumptions:
A reinforcement ratio of 2% is assumed.

Composite Lattice Prestressed Soffit Slab

Weight: 25.0 kN/m3 (kN per m2 and total height of slab)
The same weight as for standard reinforced concrete is assumed because there is also a cast in place concrete layer on top of the prefab slab.

Embodied energy: 6291 MJ/m3.

Volume of materials:
Standard Concrete: 49 %vol
High strength concrete: 49 %vol
Reinforcement: 2 %vol
Steel: 0 % vol
Timber: 0 %vol
Air: 0 %vol

Assumptions:
Thickness of precast section 100 mm, thickness of in situ concrete 100mm, reinforcement ratio 2% (Goodchild, C., Webster, R., & Elliott, K. (2009). Economic Concrete Fram Elements to Eurocode 2. Camberley UK: The Concrete Centre.)

Precast Double-Tees

Weight: 4.3 kN/m3 (kN per m2 and total height of slab)
Average of the following two examples is taken.
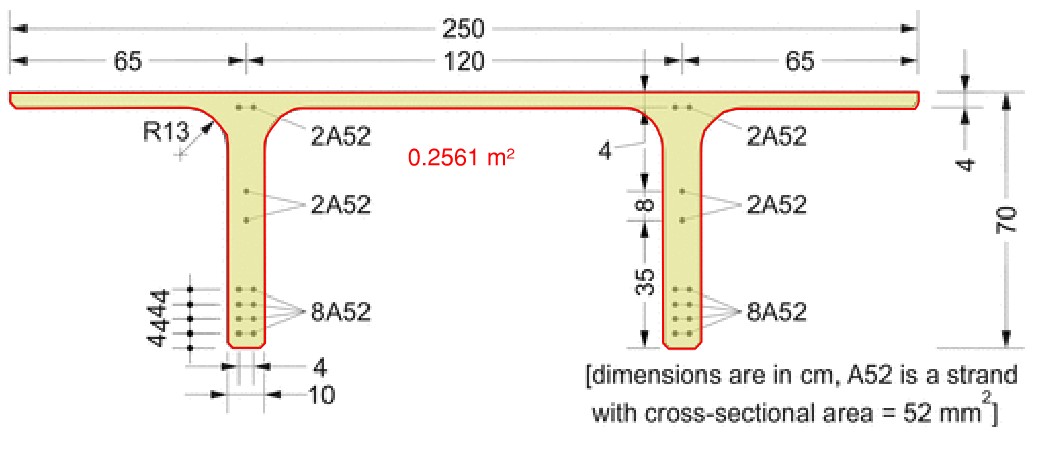
Example 1:
Area concrete: Ac= 0.2561m2
Total area: A = 0.7m * 2.5m = 1.75m2
Assuming the density of reinforced concrete: 0.2561/1.75 * 25 kN/m3 = 3.7 kN/m3

Reference: https://ascelibrary.org/doi/10.1061/%28ASCE%29EM.1943-7889.0001191

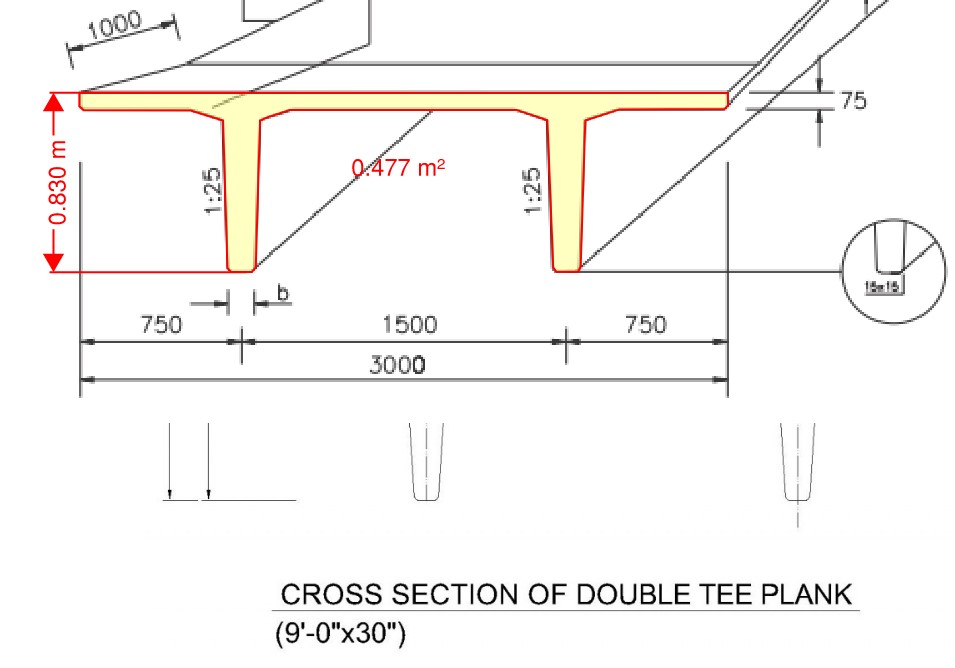
Example 2:
Area concrete: Ac= 0.477m2
Total area: A = 0.83m * 3.0m = 2.49m2
Assuming the density of reinforced concrete: 0.477/2.49 * 25 kN/m3 = 4.8 kN/m3

Reference: https://teklastructures.support.tekla.com/sv/2016i/en/ext_double_tee_ridge_beam

Embodied energy: 734 MJ/m3.

Volume of materials:
Standard Concrete: 0 %vol
High strength concrete: 16.3 %vol
Reinforcement: 0.1 %vol
Steel: 0 % vol
Timber: 0 %vol
Air: 83.6 %vol

Assumptions:
4.1kN/m3 / 25kN/m3 = 0.164
16.4% High strenght concrete Reinforced
There are 24 strands with an area of 52mm2 each.
Ratio of total volume: (24*52/1000^2)/(0.7*2.5)=0.00071 which is about 0.1%
Reference: https://ascelibrary.org/doi/10.1061/%28ASCE%29EM.1943-7889.0001191

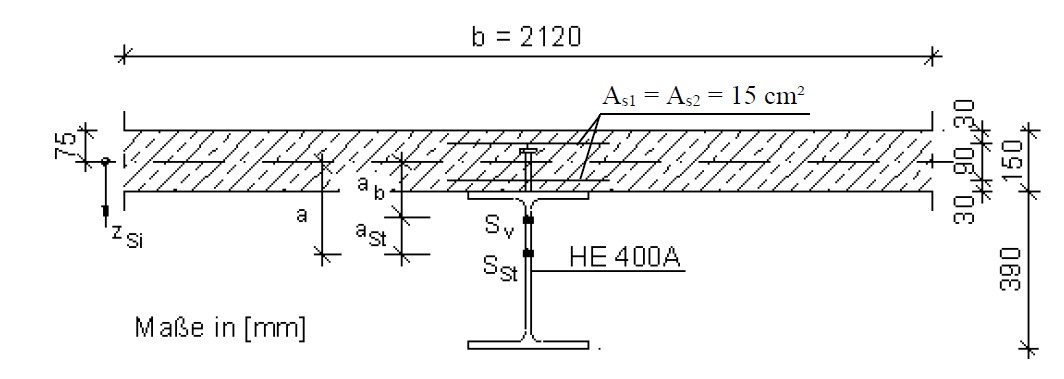
Steel-Concrete Composite Slab

Weight: 7.5 kN/m3 (kN per m2 and total height of slab)
Average value from the following two examples is taken (8.4kN/m3) and then reduced due to the shape of the decking. The decking might decrease the weight of the concrete by 29%, however, not all deckings reduce the weight that much and therfore, a reduction to 7.5kN/m3 is chosen.

Steel decking has a thickness of 1mm. (https://www.montana-ag.ch/dokumente/produkte/holorib/detailprospekt/holorib_de.pdf)

Example 1: 8.3 kN/m3
Steel decking: 1/540 *78.5kN/m3=0.14 kN/m3
Concrete: 0.15/0.54*24kN/m3 = 6.67 kN/m3
Reinforcement: 0.02*(0.15/0.54) *78.5kN/m3=0.44 kN/m3
Steel profile: 0.0159m2/m *1m / (0.54*2.12) *78.5kN/m3=1.09kN/m3”

Reference: Lecture Stahlbau III ETH Zurich

Example 2: 8.5 kN/m3
Steel decking: 1/350 *78.5kN/m3=0.22 kN/m3
Concrete: 0.1/0.35*24kN/m3 = 6.86 kN/m3
Reinforcement: 0.02*(0.1/0.35) *78.5kN/m3=0.45 kN/m3
Steel profile: 0.00414m2/m *1m / (0.35*1) *78.5kN/m3=0.93kN/m3

Reference: https://www.researchgate.net/publication/228649428

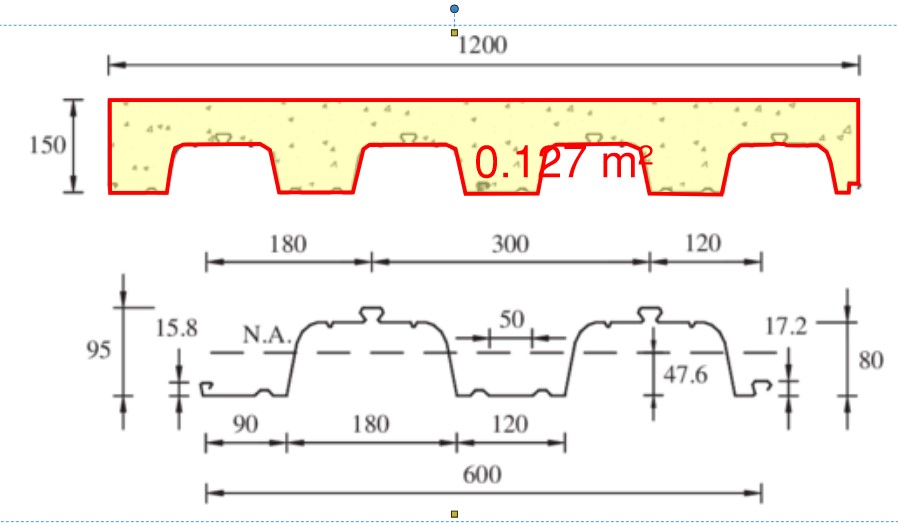
Example 3: Reduction of weight due to decking
Total area: 0.150m*1.2m= 0.18m2
Area reduction due to decking: (0.18m2 - 0.127m2)/0.18m2 = 29%
The concrete weight can be reduced up to 29% or 2kN/m3 (0.29*6.8kN/m3).

Reference: https://www.researchgate.net/publication/297736576_An_experimental_study_on_strength_and_serviceability_of_reinforced_and_steel_fibre_reinforced_concrete_SFRC_continuous_composite_slabs

Embodied energy: 4400 MJ/m3.

Volume of materials:
Standard Concrete: 28 %vol
High strength concrete: 0 %vol
Reinforcement: 0.56 %vol
Steel: 1.6 % vol
Timber: 0 %vol
Air: 69.84 %vol

Assumptions:
Steel decking: 1/540 =0.2 %vol
Concrete: 0.15/0.54 = 28 %vol
Reinforcement: 0.02*28 %vol= 0.56 %vol
Steel profile: 0.0159m2/m *1m / (0.54*2.12) = 1.4 %vol
Reference: Lecture Stahlbau III ETH Zurich

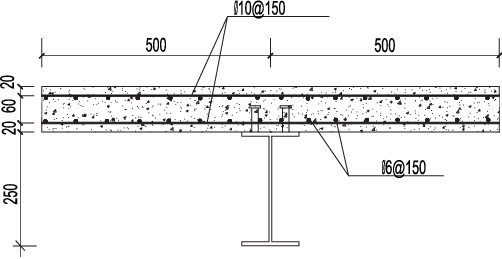
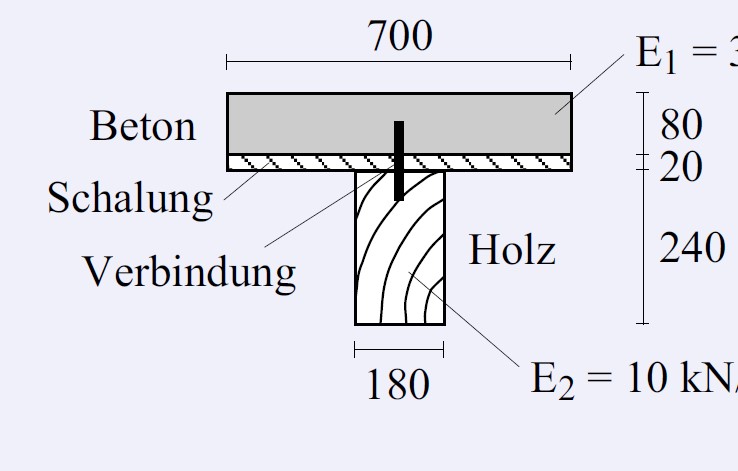
Timber-Concrete Composite Slab

Weight: 7.0 kN/m3 (kN per m2 and total height of slab)
Average value from the following three examples is taken.

Example 1: 6.8 kN/m3
Timber weight per meter: (0.7m*0.02m + 0.24m*0.18m)*3.8kN/m3 = 0.2174 kN/m
Concrete weight per meter: 0.7m*0.08m*25kN/m3 = 1.4 kN/m
Total weight: (0.2174kN/m + 1.4kN/m)/(0.7m*0.34m) = 6.8kN/m3

(0.7m*0.08m*25kN/m3 + )/(0.7m*0.34m) = 6.8kN/m3

Reference: Lecture Holzbau I/II ETH Zurich

Example 2: 3.6 kN/m3
Timber weight per meter: (1.1m*0.02m+ 0.26m*0.08m)*3.8kN/m3 = 0.16 kN/m
Concrete weight per meter: 1.1m*0.04m*25kN/m3 = 1.1 kN/m
Total weight: (0.16kN/m + 1.1kN/m) / (1.1m*0.32m) = 3.6 kN/m3

Reference: https://www.sciencedirect.com/science/article/pii/S0263822317317397

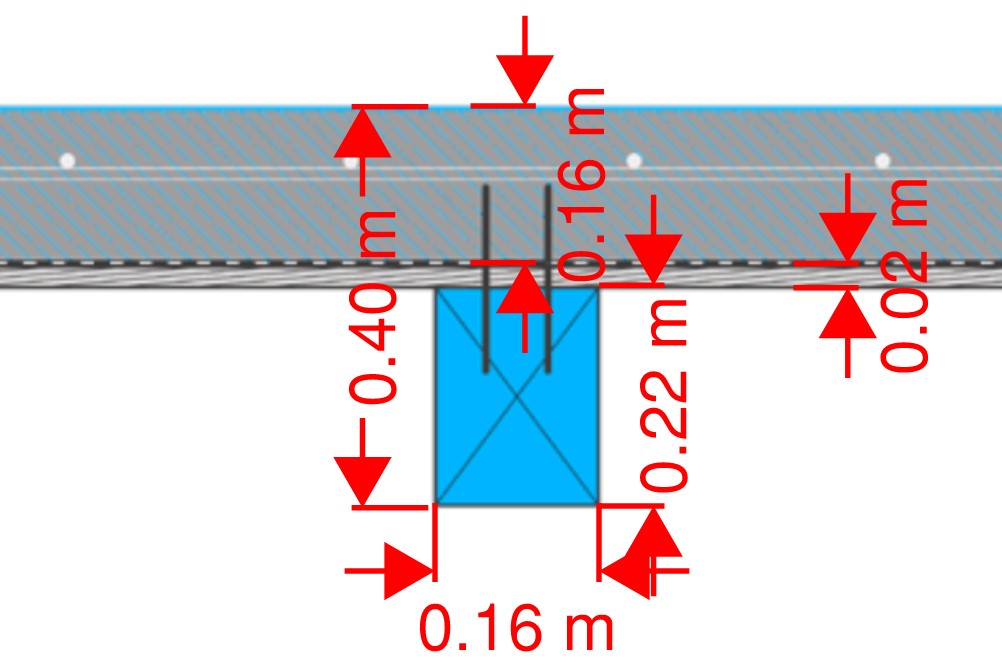
Example 3: 10.5 kN/m3
Timber weight per meter: (0.02m*1m + 0.16m*0.22m)*3.8kN/m3 = 0.21 kN/m
Concrete weight per meter: 0.16m*1m*25kN/m3 = 4.0 kN/m
Total weight: (0.21kN/m + 4.0kN/m) / (1m*0.4m) = 10.5 kN/m3

Reference: https://www.bauwion.de/wissen/rohbau/geschossdecke/114-holz-beton-verbunddecken

Embodied energy: 1127 MJ/m3.

Volume of materials:
Standard Concrete: 23.5 %vol
High strength concrete: 0 %vol
Reinforcement: 0.12 %vol
Steel: 0 % vol
Timber: 24 %vol
Air: 52.38 %vol

Assumptions:
Timber: (0.18m*0.24m + 0.02m*0.7m)/(0.7m*0.34m) = 24.0 %vol
Concrete: (0.7m*0.08m)/(0.7m*0.34m)= 23.5 %vol
Reinforcement: Assume 0.5% of concrete volume = 0.12 %vol
Reference: Lecture Holzbau I/II ETH Zurich

Holedeck

Weight: 5.0 kN/m3 (kN per m2 and total height of slab)
Average value from the following examples is taken.
htot=50 cm (ink. 5cm topping), width bottom 150mm and 200mm
6.0 kN/m3 (average of those two widths)
htot=35 cm (ink. 5cm topping), width bottom 150mm and 200mm
3.8 kN/m3 (average of those two widths)

Embodied energy: 1041 MJ/m3.

Volume of materials:
Standard Concrete: 19.6 %vol
High strength concrete: 0 %vol
Reinforcement: 0.4 %vol
Steel: 0 % vol
Timber: 0 %vol
Air: 83.6 %vol

Assumptions:
5kN/m3 / 25kN/m3 = 0.20
20% of volume is reinforced concrete.

Slim-Floor

Weight: 18.0 kN/m3 (kN per m2 and total height of slab)
The weight of reinforced concrete (25kN/m3) is reduced to 18kN/m3 due to the decking which reduces the weight up to 29%.
0.150m*1.2m= 0.18m2
(0.18m2 - 0.127m2)/0.18m2 = 29%

Reference: https://www.researchgate.net/publication/297736576_An_experimental_study_on_strength_and_serviceability_of_reinforced_and_steel_fibre_reinforced_concrete_SFRC_continuous_composite_slabs

Embodied energy: 5948 MJ/m3.

Volume of materials:

Standard Concrete: 98 %vol
High strength concrete: 0 %vol
Reinforcement: 1.3 %vol
Steel: 0.7 % vol
Timber: 0 %vol
Air: 0 %vol

Assumptions:
The steel decking is about 1mm thick which is about 0.7% of the volume (1/150). The total amount of reinforcement and steel decking is assumed to be 2%. Therefore, the reinforcement itself is 1.3% vol.
(https://www.montana-ag.ch/dokumente/produkte/holorib/detailprospekt/holorib_de.pdf)

Voided Biaxial Slab

Weight: 18.0 kN/m3 (kN per m2 and total height of slab)
The weight of reinforced concrete (25kN/m3) is reduced to 18kN/m3 due to the voided elements.
Reference:
18 kN/m3 (h=50cm). (https://www.cobiax.com/ch/de/produkte/)
17.5 kN/m3 (reduction by about 30%). (https://www.voidedconcrete.com/system)

Embodied energy: 4200 MJ/m3.

Volume of materials:

Standard Concrete: 70 %vol
High strength concrete: 0 %vol
Reinforcement: 1.4 %vol
Steel: 0 % vol
Timber: 0 %vol
Air: 28.6 %vol

Assumptions:
About 30% reduction of concrete and reinforcement due to voided elements.

Laminated Timber Slab

Weight: 3.8 kN/m3 (kN per m2 and total height of slab)
Reference:
3.8 kN/m3 (https://wissenwiki.de/Brettschichtholz)
3.85 kN/m3 (https://www.binderholz.com/fileadmin/user_upload/pdf/produkte/brettschichtholz-kvh.pdf)
3.8 kN/m3 (Swiss Code SIA 265)

Embodied energy: 1300 MJ/m3.

Volume of materials:
Standard Concrete: 0 %vol
High strength concrete: 0 %vol
Reinforcement: 0 %vol
Steel: 0 % vol
Timber: 100 %vol
Air: 0 %vol

Assumptions:
100% of this slab is timber.

References

Source 1: Ashby, M. (2013). Materials and the Environment. Oxford UK: Elsevier.

Source 2: Hammond, G.P. and C.I. Jones (2008), Embodied energy and carbon in construction material. Bath UK: Proc. Instn Civil. Engrs:Energy.

Source 3: Alcorn, A. (2001). Embodied Energy and CO2 Coefficents for NZ Building Materials. Wellington NZ.